
Подробности в https://magazine.neftegaz.ru/articles/tsifrovizatsiya/682079-entropiynyy-kompas-dlya-analiza-byudzheta-ekonomicheskoy-sistemy/

Подробности в https://magazine.neftegaz.ru/articles/tsifrovizatsiya/682079-entropiynyy-kompas-dlya-analiza-byudzheta-ekonomicheskoy-sistemy/
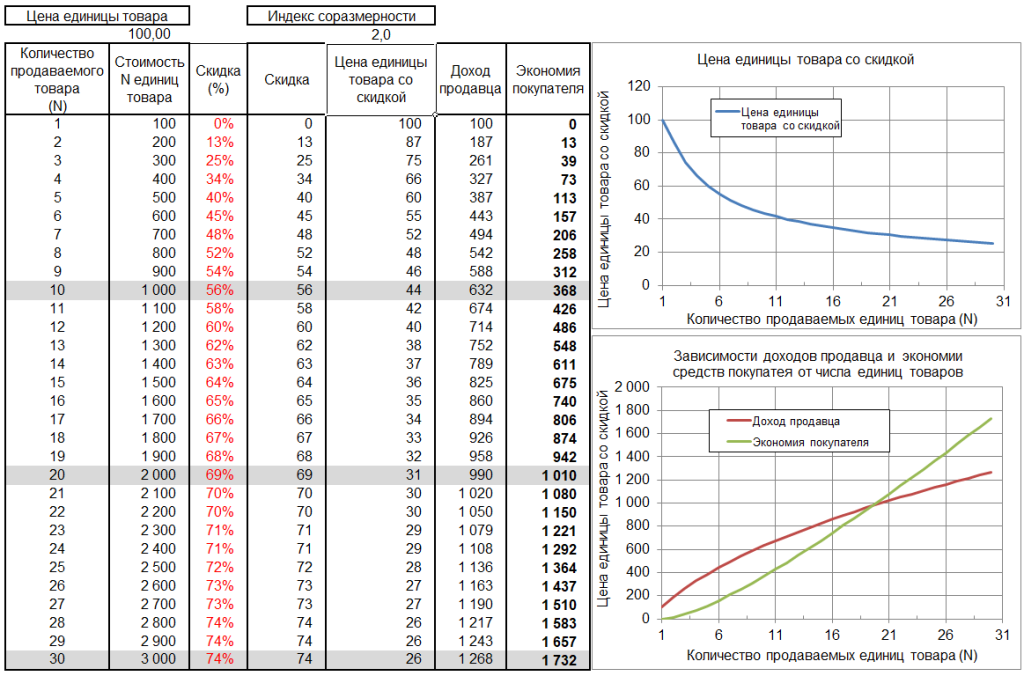
Ключевым вопросом организации торговли товарами является прогрессивная система скидок побуждающая покупателя приобретать у продавца больший объем продукции.
В частности, продавец предлагает покупателю приобретать товар со скидкой при покупке более одной единицы товара. То есть, если покупатель приобретает несколько единиц товара, то цена каждой дополнительно приобретаемой единицы товара уменьшается на величину скидки. Таким образом, поощряется желание покупателя приобретать больший объем товара.
На прилагаемом рисунке приведены таблица и графики, отражающие результаты расчета выручки продавца и экономии средств покупателя в зависимости от различного объема продаваемого (приобретаемого) товара.
Характерной чертой различных экономических систем является их способность производить полезный продукт, используя внешние и собственные ресурсы. При этом жизнеспособные экономические системы изменяют свое состояние, реагируя на воздействие различных дестабилизирующих факторов. Естественно предположить, что последствия изменений состояния экономической системы могут иметь как позитивный, так и негативный характер. Особенно опасны небольшие и малозаметные негативные изменения, имеющие тенденцию к накоплению отрицательного эффекта. Ибо накопление негативных изменений может незаметно привести экономическую систему к кризисному состоянию, купирование которого потребует дополнительных объемов ресурсов и временных затрат. Для того чтобы заблаговременно выявлять зарождение подобного рода проблем, нужен особый индикатор, реагирующий на широкий спектр изменений состояния экономической системы. При этом наряду с просто фиксацией изменений необходимо также определять их величину и направленность отклонения экономической системы от штатного режима работы. Для того чтобы создать требуемый индикатор изменений состояния экономической системы, необходимо, прежде всего, определить подходящий источник данных и методологию его обработки. Наибольшими преференциями при выборе источника данных, по целому ряду причин, обладают расходы денежных средств, поскольку именно они отражают широкий спектр изменений состояния экономической системы. Кроме того, расходы денежных средств оказывают управленческое влияние на состояние экономической системы, непосредственно не являясь фактором производства. Такого рода особая роль и позиция расходов денежных средств отражена на упрощенной двухсекторной функциональной схеме жизненного цикла экономической системы
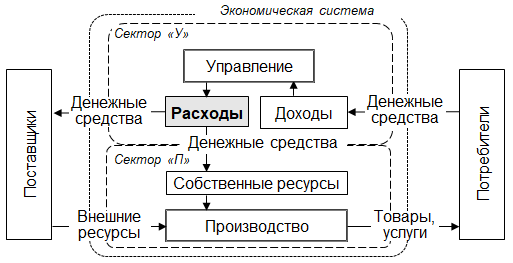
Данная схема позволяет рассматривать совокупность расходов денежных средств как индикативно-управленческую подсистему, позволяющую выявлять и купировать зарождение негативных тенденций в состоянии экономической системы.
Читать далееПростейшей и наиболее распространенной формой оформления числовых рядов, используемых в качестве исходных данных для анализа совокупности расходов, является таблица, состоящая из двух колонок. В левой колонке таблицы приводится название или порядковый номер строки (n), а в правой – значение соответствующего элемента статистического ряда несгруппированных данных (Gn). Данная форма представления может быть трансформирована в иные формы с целью реализации более детального сравнения конкретных свойств экономической системы. На рисунке приведены три формы представления числового ряда {G}={G1, G2,…, GN), позволяющие сравнивать с денежной точки зрения состояния экономических систем в разные моменты времени.
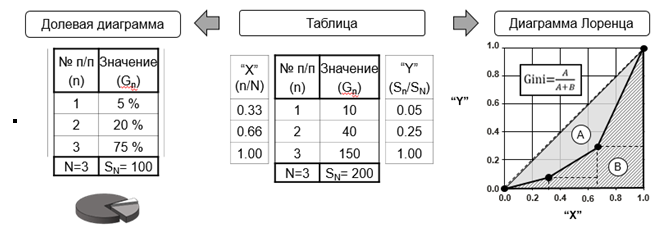
Табличная форма, долевая диаграмма и диаграмма Лоренца позволяют сравнивать числовые ряды как системы:
В первом случае сравнение числовых рядов может быть реализовано простым построчным вычитанием. Поскольку данная форма не предполагает обязательности смысловой однородности элементов числового ряда, то результаты сравнения носят исключительно построчный характер. Кроме того, табличная форма носит открытый характер. То есть, все числа известны.
Во втором случае возникают дополнительные требования к элементам числового ряда. А именно, все элементы должны иметь общий смысл, который позволяет корректно использовать арифметические операции. То есть, например, трансформировать числовые значения в проценты «%»: вес в одной строке/общий вес, длину в одной строке/общую длину, время в одной строке/общее время, денежная единица/сумму, Gn/SN. Таким образом делением на общую сумму реализуется возможность визуального представления неравномерности построчного распределения элементов числового ряда в виде долевой диаграммы.
Таким образом, в методологическом и практическом смысле реализуется возможность количественного сравнения числовых рядов с разными значениями SN и равными N.
К сожалению приходится констатировать часто встречающее некорректное использование долевых диаграмм при разных значениях N, которое может привести к неверным выводам.
Помимо долевой диаграммы при условии однородности смысловой принадлежности строк становятся доступными операции агрегирования (суммирования и вычитания) значений элементов числового ряда, указанных в разных строках таблицы.
Отметим, и еще одну особенность долевой диаграммы. Перевод исходных данных в проценты фактически повышает уровень информационной защиты результатов анализа, поскольку по виду долевой диаграммы нельзя определить абсолютные значения конфиденциальной денежной и управленческой информации.
Однако, при всех достоинствах долевых диаграмм последние не позволяют сравнивать числовые ряды с разными количествами строк N и разными значения сумм SN. Проблема сравнения числовых рядов с разными значениями N и SN решается профильными специалистами использованием диаграмм Лоренца, представляющих числовые ряды в виде кусочно-линейного графика (диаграмма Лоренца). Очевидно, что все диаграммы Лоренца располагаются между равномерным («А» — диагональ квадрата) и существенно неравномерным («М» уголок квадрата) вариантами распределений значений соответствующего числового ряда. Методологические преимущества диаграмм Лоренца расширяются параметром неравномерности в виде коэффициента Джини (Gini), который позволяет упорядочить диаграммы Лоренца в интервале (0.0; 1.0). Однако, коэффициент Джини последний не дает ответа на вопрос о предпочтительности одних числовых рядов над другими. Вопрос о том, чем один числовой ряд «предпочтительней» другого, остается открытым. Ответ на данный вопрос позволил бы изучать динамику различных систем, состояние которых характеризовалось бы конкретным числовым рядом. В этой связи становятся целесообразными попытки поиска нового параметра числовых рядов как аналога энтропии. То есть, если бы удалось рассчитать энтропию состояний системы с характерными числовыми рядами, то предпочтительным было бы состояние с большим значением энтропии. Такая возможность носит характер диагностики, позволяющей упорядочить состояния различных систем и сделать прогноз развития событий. Однако, данная возможность стала бы полноценным практическим инструментом управления системами в случае, если бы удалось сделать обратный ход. А именно, однозначно связать энтропию с табличной формой представления числового ряда. Иными словами так изменить исходный числовой ряд, чтобы увеличить энтропию соответствующей системы. Итак, «золотым ключиком» к реализации возможности диагностики и управления состояниями систем стало бы функциональная связь энтропии и неравномерности распределения значений числовых рядов.

X I X МЕЖДУНАРОДНАЯ ШКОЛА-СИМПОЗИУМ
Симферополь-Судак, 14-27 сентября 2025
(ПЕРВОЕ ИНФОРМАЦИОННОЕ СООБЩЕНИЕ)
ТЕМАТИЧЕСКИЕ НАПРАВЛЕНИЯ ШКОЛЫ—СИМПОЗИУМА
ПРОГРАММНЫЙ КОМИТЕТ
Председатель:
Апатова Н. В., д.э.н., д.п.н., профессор (КФУ им. В. И. Вернадского, Симферополь),
Члены комитета:
Альсевич В. В., к.ф.-м.н., профессор (БГУ, Минск),
Голембиовский Д. Ю., д.т.н., профессор (Промсвязьбанк, Москва),
Горидько Н. П., к.э.н., доцент (ИПУ РАН, Москва),
Жуковский В. И., д.ф.-м.н., профессор (МГУ им. М. В. Ломоносова, Москва),
Карасев В. В., к.т.н., с.н.с. (ИПМаш, С.-Петербург),
Клейнер Г. Б., д.э.н., профессор, член-корр. РАН (ЦЭМИ РАН, Москва),
Колесов Д. Н., к.э.н., доцент (СПбГУ, С.-Петербург),
Краснова В. В., д.э.н., профессор (ДонГУ, Донецк),
Лившиц В. Н., д.э.н., профессор (ФИЦ ИУ РАН, Москва),
Нижегородцев Р. М., д.э.н. (ИПУ РАН, Москва),
Орлова Е. Р., д.э.н., профессор (ФИЦ ИУ РАН, Москва),
Рогов М. А., к.э.н., доцент (РАНХиГС, Москва),
Смирнов Н. В., д.ф.-м.н., профессор (СПбГУ, С.-Петербург),
Суслов В. И., д.э.н., профессор, член-корр. РАН (ИЭОПП СО РАН, Новосибирск),
Сухарев О. С., д.э.н., профессор (ИЭ РАН, Москва).
ОРГАНИЗАЦИОННЫЙ КОМИТЕТ
Председатель:
Сигал А. В., д.э.н., профессор (КФУ им. В. И. Вернадского, Симферополь),
Заместитель председателя:
Королёв О. Л., к.э.н., доцент (КФУ им. В. И. Вернадского, Симферополь),
Члены комитета:
Бакуменко М. А., к.э.н., доцент (КФУ им. В. И. Вернадского, Симферополь),
Друзин Р. В., к.э.н., доцент (КФУ им. В. И. Вернадского, Симферополь),
Куссый М. Ю., к.э.н., доцент (КФУ им. В. И. Вернадского, Симферополь),
Ремесник Е. С., к.э.н., доцент (КФУ им. В. И. Вернадского, Симферополь).
АДРЕС ОРГКОМИТЕТА
Сигал Анатолий Викторович, профессор кафедры бизнес-информатики и математического моделирования, Физико-технический институт ФГАОУ ВО «КФУ им. В. И. Вернадского», просп. Академика Вернадского, 4, Симферополь, Республика Крым, Россия, 295007.
Контактный телефон: +7(978) 76 96 365 (моб.). E-mail: ksavo.conf@gmail.com